2019-09-23

VAE(Variational Auto Encoder)で猫が復元できなかった話

Keras python Deep Learning

はじめに

couseraでBayesian Methods for Machine Learningを受けているんですが、その中で出てきたVAE(Variational Auto Encoder)で少し試してみたいことがあったのでその実験記録になります。

参考文献

VAEの理論や位置付けについては下記資料が参考になります。

VAEについて

f:id:rmizutaa:20190923122955p:plain

VAEは上図のような構造をもつモデルで、入力画像の特徴量をEncoderによって低次元の潜在変数に押し込め、その潜在変数を用いて元の画像を復元するというモデルになります。低次元化された潜在変数では入力画像の復元をするのに重要な特徴量のみを抽出できるため、次元削減やノイズ除去に利用されます。また入力と出力の誤差を用いて異常検知にも利用できます。

この構造はAuto encoderと同じなのですが、VAEはこの潜在変数の部分を確率分布としている点が特徴になります。潜在変数を確率分布とするメリットとしては、ノイズ項があるため同じ入力でも異なる出力となり全く新しい出力を生成できること、潜在変数が連続的な分布であるために、例えばある特徴をもつ出力を生成するために潜在変数を調整できることや、未知の入力に対する挙動も担保できる点が挙げられます。

実験

kaggleのDogs vs. Catsのデータを使って猫画像だけを学習させ、猫以外の画像を異常と検知するようなモデルの作成を目指します。

VAE+CNNの実装がkerasの公式にあるのでこれをベースにします。

https://github.com/keras-team/keras/blob/master/examples/variational_autoencoder_deconv.py

上記のリンクのものから入出力やCNNの層の数などを今回のデータに合わせるために少し変更しました。ネットワークは四段のCNNで構成し、潜在変数の数は256としました。サンプルサイズはtrainデータは8000、validデータは2000です。実験環境はgoogle colaboratoryです。

作成したEncoderのネットワークは以下になります。 f:id:rmizutaa:20190923122850p:plain

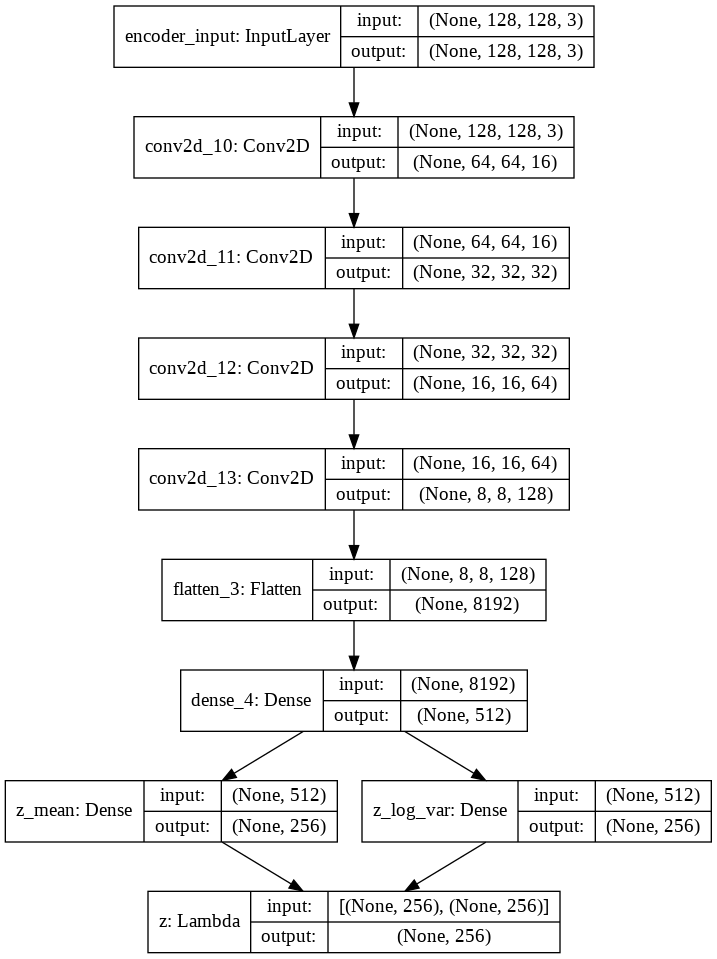
Decoderのネットワークは以下になります。 f:id:rmizutaa:20190923122913p:plain

ここではコードは割愛しますが、使用したものはこちらになります。

github.com

ある程度学習できたようなので、このモデルの精度を確認するためにいくつか入力画像と出力画像を見比べてみます。左が入力、右が出力になります。

f:id:rmizutaa:20190923122935p:plain

あまり復元がうまくできていません。輪郭がうっすらわかる程度です。精度の問題かと思ってネットワークの層の数やパラメータ、潜在変数の数の変更、画像のグレースケール化などを試してみましたが結果に大きな変化はみられませんでした。reconstruction errorで犬画像との差を見ようと思っていたのですが、それ以前の問題でした。

この原因としては、学習画像によるばらつきが大きすぎるのが原因かと考えています。よくサンプルとして使われるmnistや顔画像のデータセットは画像のどの部分になにがあるかが比較的明確で、画像毎のばらつきが小さいデータセットだと思います。それらと比較すると今回入力として用いた画像は猫のサイズ、位置や向き、背景、猫種など同じ猫でも入力画像毎の違いが大きく、潜在変数の少ないパラメータでは画像の特徴を表し切ることができなかったのかなと思いました。 (とはいえNNはあまり得意でないのでプロがやったらできるのかもしれませんが…)

まとめ

VAEで猫画像だけを学習させた異常検知のモデルは作れなかった
VAEを正しく使用する際にはネットワークのチューニングや入力画像の選定が必要だと感じた

2019-07-21

変数間の関係性が見たい(偏相関とGraphical Lasso)

python 統計

はじめに

データの変数間の関係性を明らかにしたいというケースは多いと思います。その場合相関や散布図をみるのが一般的ですが、交絡やノイズが多いケースなどそれだけでは不十分な場合もあるため、その場合にも対応できそうな手法を試してみます。試す手法は偏相関行列とGraphical Lassoです。

参考資料

・統計: 偏相関係数で擬似(無)相関の有無を調べる - CUBE SUGAR CONTAINER

・【PyStan】Graphical LassoをStanでやってみる。 - Qiita

・岩波データサイエンス Vol．5

データの準備

NPBのサイトから2013~18年の5年分の打者個人成績をスクレイピングします。

initflag=1
for year, league in itertools.product(range(2014, 2019), ['p', 'c']):
    url=f'http://npb.jp/bis/{year}/stats/bat_{league}.html'
    tables = pd.read_html(url)
    df_with_header = tables[0]
    df = df_with_header.iloc[2:,:] #使用カラム
    df.columns=df_with_header.iloc[1,:] #列名
    df["year"]=year
    df["league"]=league
    if initflag==1:
        output=df
        initflag=0
    else:
        output=pd.concat([output,df])
    time.sleep(1) #サーバに気をつかう

output.to_csv("baseball_stats.csv",index=False)

取得したデータ以下のような感じ。

f:id:rmizutaa:20190721110852p:plain

相関と偏相関

塁打や出塁率など他の変数から算出が可能な変数を省き、変数の相関をみてみます。

f:id:rmizutaa:20190721110914p:plain

結構それぞれの変数間の関係性は妥当に見えますが、得点と三振や、盗塁と盗塁刺の相関が高いなど解釈が難しい数値もあります。

これらは実際は他の共通変数が相関している影響による疑似相関ではないかと考えられます。前者では打席数の影響が、後者は盗塁企画数みたいなものの影響でこれらの変数に相関があるように見えている可能性が高いです。

他の変数の影響を考慮した場合の相関関係をみる偏相関係数というものがあります。式としては以下のような形で表されます。

$p_{ij} = \frac{-\lambda_{ij}}{\sqrt{\lambda_{ii}\lambda_{jj}}}$

ここで、 $p_{ij}$ は偏相関行列の要素で、 $\lambda_{ij},\lambda_{ii},\lambda_{jj}$ は精度行列（分散共分散行列の逆行列）の要素になります。

計算した偏相関行列は以下のようになりました。

f:id:rmizutaa:20190721110936p:plain

得点と三振については相関が小さくなり、盗塁と盗塁刺については負の相関があるという結果になりました。盗塁企画数は今回のデータには含まれていませんが、３塁打や犠打の数である程度代用できたのではないかと思います。一方で、打点と本塁打に負の相関があるなど偏相関行列にすることで直感的におかしな部分も生じています。

Graphical Lassoを使ってみる

本当に関係性の高い特徴量だけを使えば少し違った結果が出るのではないかと思いGraphical Lassoも使ってみます。Graphical Lassoは変数間の関係を推定するために、ガウシアングラフィカルモデルにL1正則化の考え方を応用したものになります。

lassoを使うため標準化を行い、またGraphical Lassoは多変量正規分布を仮定しているため変数にboxcox変換をかけて正規分布に近づけます。

X_gl = pd.DataFrame(StandardScaler().fit_transform(df.iloc[:,3:-2].drop(["塁　打","打　数","長打率","出塁率","試　合"],axis=1)))
pt = PowerTransformer()
df_gl = pd.DataFrame(pt.fit_transform(X_gl))

Graphical Lassoを使用します。

alpha = 0.2 # L１正則化パラメーター
model = GraphLasso(alpha=alpha,
                     max_iter=100,                     
                     verbose=True,
                     assume_centered = True)
model.fit(X_gl)
cov_ = model.covariance_ # 分散共分散行列
prec_ = model.precision_ # 精度行列

相関は以下のような形に。色が暗い領域が増え関係性の強い項目がみやすくなりました。

f:id:rmizutaa:20190721111018p:plain

交絡の影響を除くため先ほどと同様に計算を行い、偏相関行列は以下のようになりました。

f:id:rmizutaa:20190721111030p:plain

問題とした部分はGraphical Lassoを用いない場合とあまり変わりませんでした。相関値で確認すると打点と本塁打の項目は共に犠打と負の相関が、三振と正の相関があるためこれらの影響による疑似相関だと判定されている気がします。犠打を減らすと打点や本塁打が増えるはずはないので、偏相関係数の算出も機械的に行うのではなく疑似相関にあたりをつけて個別に実施するのが良さそうです。

まとめ

・今回のように変数の意味がわかるデータセットの場合は、全体の変数で偏相関行列を作っても不自然な部分が出るため、疑似相関が出ている変数とその原因にあたりをつけてその変数のみで処理を行った方が良いと思った。
・Graphical Lassoは多変量正規分布を仮定していることを考えると、センサデータ等の変数同士の関係性の理解が難しく、ノイズが乗りやすいデータに適用が向いていそうだと思った。

使用したコードは以下になります。

github.com

2019-06-30

機械学習における欠損値補完について考える

python 機械学習統計

※この記事で使用している多重代入法のパッケージは正式な多重代入法の枠組みとは異なりますのでご注意願います。

はじめに

最近多重代入法という欠損値補完の手法があることを知りました。統計学の界隈では欠損値補完は多重代入法を使用するのがベターのようですが、機械学習の文脈ではあまりその手法が使用されている形跡がなかったので、なぜそうなのか調査・実験した結果を記述します。

参考資料

欠測データ処理: Rによる単一代入法と多重代入法

欠損値について

欠損には大きく以下の３種類があります。

・MCAR(Missing Completely At Random):完全にランダムに欠損

・MAR(Missing At Random):観測データに依存する欠損

・MNAR(Missing Not At Random):欠損データに依存する欠損

多くの学習器は欠損値を入力できないので欠損値に対応する必要がありますが、欠損した行を削ったり平均値埋めなどをするとバイアスが生じるためにそうならないような方法が必要となります。欠損値の補完方法としてはいろいろ手法があるのですが、今は多重代入法を用いるのがベターなようです。パッケージとしてはRのmiceが一番メジャーでしょうか。考え方としては欠損している変数を他の欠損していない変数を用いて推定するというものです。 miceで推定するアルゴリズムは線形モデルが使用されることが多いようです。詳細を知りたい方は参考資料を参照するのが良いかと思います。多重代入法はMARに対して最も効果がありますが、MNARの場合でも補助変数を入れてMARに近づければ効果が出るようです。

機械学習における欠損処理

機械学習で使用頻度の高いlightgbmやxgboostといった勾配ブースティングを用いる場合、デフォルト設定だと欠損値を補完しなくてもlossが下がるように欠損値の部分が処理されます。詳細は以下資料の3.2項を参照してください。 http://mlexplained.com/2018/01/05/lightgbm-and-xgboost-explained/

このアプローチの場合、欠損値は補完されるわけではなく、欠損という特徴をlossがより下がる方にsplitすることになります。処理的に欠損値のジャンルでいうとMNARのケースに最も有効に働きそうです。

実験

多重代入法が回帰や分類に効果があるかを確認するため、様々な欠損値補完を用いた場合の精度の比較を行います。欠損値補完はRだとmiceを使用するケースが多いようですが、今回はpythonを使いたかったのでsklearnのIterativeImputerとfancyimputeを用いて欠損値補完を行いました。IterativeImputerの方は19年6月ではまだ実験段階のもののようなので使用する場合は注意してください。miceとこれらパッケージの主な違いは補完するアルゴリズムをいろいろ変えている点になります。

データはMelbourne Housing Marketを使います。このデータセットはメルボルンの住宅の特徴と価格が入ったデータセットになっており、複数の変数で欠損が存在しているデータになります。

このデータを用いて、部屋数や築年数などの住宅の特徴から価格を予測するモデルを作成します。手順としては最低限の前処理後、各方法で欠損値補完を行い、 lightgbmで学習した5foldの平均RMSEを比較しました。

コードは割愛します。使用したコードは以下になります。

github.com

結果は以下のようになりました。 (I)がsklearnのIterativeImputerを用いたもので、(F)がfancyimputeを用いたものになります。

欠損値補完方法	RMSE
補完なし	300058
baysian ridge(I)	308926
ExtraTreesRegressor(I)	308560
KNeighborsRegressor(I)	308190
MatrixFactorization(F)	312793
BiScaler(F)	386955
SoftImpute(F)	305534

補完を用いず欠損値をそのままlightgbmに入れたものが最も性能が良い結果となりました。下手に値が入っているよりも欠損であることがわかる方がlightgbmとしてはうれしいようです。今回の住宅のデータセットだと確かに欠損していることが推定の手段として役立つ(条件が悪すぎで載せられない、古いため情報が残っていない等)場合が考えられるので、この結果にそれほど違和感はないかと思いました。仕組み的に欠損値がMNARである場合にはそのまま欠損を入れた方がよく、 MARやMCARである場合には欠損であることに情報量はないので、補完した方が性能がよくなる可能性があるかなと思いました。

まとめ

統計学における欠損補完の目的はバイアスなく統計処理を行うものであり、機械学習の欠損処理の目的は回帰・分類精度を高めることが目的であるため、欠損処理についても目的別で考える必要があると思いました。
多重代入法のような欠損値補完はどちらかというと解釈のために使用する場合に役立つと考えられ、機械学習を用いる場合でも解釈性を求める場合は欠損値をどう埋めるかは問題になると思いました。例えばSHAPとかLIMEだと線形モデルを用いるのでこの部分は影響してくると思うのですがどうなっているかが気になりました。

2019-06-10

ランチ最適化問題(バンディットアルゴリズム編)

python 数理最適化

はじめに

日々の生活を営む上で、ランチをどこで食べるかということは非常に重要な問題です(2回目)。

前回はこの問題を最適停止問題と捉えて探索と活用の最適点探索を行いましたが、最適停止問題では一度見逃した店はもう選択できないという制約がありました。

飲食店で考えると一度利用した店をもう一度利用することが可能なので、この問いに対してはバンディットアルゴリズムを用いた方が適していると考えられます。そのため今回はバンディットアルゴリズムを用いた場合の実験を行います。

参考図書

バンディットアルゴリズムについて

以下のスライドが分かりやすいです。

https://www.slideshare.net/greenmidori83/ss-28443892

バンディットアルゴリズムは例えばカジノのスロットマシーンのように、報酬が不明な複数の選択肢がある場合にどのように選択を行えば累積報酬を最大にできるかを解くアルゴリズムで、インターネット広告配信や推薦システムで用いられています。複数の解き方があり、ε-greedy、UCB、Thompson Samplingあたりが有名です。

ABテストとの違いが疑問として出やすいですが、ABテストはAとBのどちらが優れているかを決めるものであり、バンディットアルゴリズムはABテストの期間中の報酬を最大になるようにAとBの出現比率を調整するものなので、目的が異なるものになります。

実験

ベイズ統計の枠組みを利用しているThompson Samplingが面白そうだったので、今回はThompson Samplingを用いて以下の２通り場合の実験を行います。

報酬がベルヌーイ分布に従う場合
報酬が平均・分散未知の正規分布に従う場合

報酬がベルヌーイ分布に従う場合のThompson Sampling

仮定として、1回の試行につき各店舗で得られる利得が0（まずい）か1（うまい）の二値とし、各店舗のもつ確率は一定であるとします。この条件における一定の試行回数における合計利得を最大化するケースです。

今回対象店舗を10店舗とし、各店舗の期待値は以下のようになっているものとします。
[0.2,0.2,0.2,0.2,0.4,0.4,0.4,0.4,0.45,0.5]
10番目の店舗の期待値が最も大きく0.5であるため、10番目の店舗だけを選択し続けるのが最適解となります。

実施する手順は以下になります。

各店舗の利得予測値をベータ分布からランダムサンプリング
最も利得の大きい店舗を選択、その店舗の利得(0か1)を観測
選択店舗のベータ分布の事前確率を更新
1~3を試行回数分繰り返し

コードは以下のようになります。

def thompson_bernoulli(armparams,T,ps):
    reward=0
    cumulative_reward=[]
    
    for i in range(1,T):
        #ベータ分布よりランダムサンプリング
        thetas = [np.random.beta(a=armparams[index,2], b=armparams[index,3]) for index in range(len(ps))]
        #値が最大のアームを選択
        index=max(enumerate(thetas), key=lambda x: x[1])[0]
        result = binomial(n=1, p=ps[index])
        if result == 1:
            armparams[index,0]+=1
            armparams[index,2]+=1
        else:
            armparams[index,1]+=1
            armparams[index,3]+=1
        
        reward+=result
        cumulative_reward.append(reward)
    return pd.Series(cumulative_reward)/T

#試行回数
T=10000

#アームの数
armnum=10

#それぞれのアームの正解率(当てたいもの)
ps=[0.2,0.2,0.2,0.2,0.4,0.4,0.4,0.4,0.45,0.5]

#初期値
armparams=np.zeros((armnum,4))
armparams[:,2]=1 #alpha
armparams[:,3]=1 #beta

#実行
thompson_bernoulli(armparams,T,ps).plot()

正規化した累積報酬は0.5にかなり近くなりました。

f:id:rmizutaa:20190609213057p:plain

それぞれの店舗のパラメータを確認します。

resultparams=pd.DataFrame(armparams)
resultparams.columns=["win_count","lose_count","alpha","beta"]
resultparams

f:id:rmizutaa:20190609213110p:plain

win_countがその店舗が当たりだった回数でlose_countがハズレだった回数です。 win_count+lose_countがその店舗が選択された回数になります。確率値が0.2の店舗1~4は30回前後しか選択されず、確率値が0.4~0.45の店舗5~9は100~200回ほど選択されています。最も選択したい確率値が0.5の店舗10は9000回近くと最も選択できていることがわかります。

各店舗の事後分布を確認します。

#事後分布
from scipy import stats
x = np.linspace(0,1,100)
plt.figure(figsize=(10,6))
num=1
for a,b in zip(armparams[:,2], armparams[:,3]):
    beta_pdf = stats.beta.pdf(x, a, b)
    plt.plot(x,beta_pdf,label=num)
    num+=1
plt.legend()
plt.show()

ベータ分布は更新されるごとに分布が尖っていくので、あまり選択されていない店舗1~4は分布がなだらかで、最も選択された店舗10ではかなり尖った形になります。この分布からランダムサンプリングした値を用いるので店舗10を選ぶ確率が非常に大きくなります。

f:id:rmizutaa:20190609213126p:plain

報酬が平均・分散未知の正規分布に従う場合のThompson Sampling

店舗から得られる利得は0(まずい)か1(うまい)の2値ではなく、その中間の値もあったり同じ店舗でもその日の食材調達状況によって変化したりする場合もあるので実際は幅をもつ連続値であると考える方が自然です。上記を踏まえ店舗の報酬を正規分布と仮定したケースを考えます。

今回対象店舗を4店舗とし、各店舗の期待値と分散は以下のようになっているものとします。
[[0,0.3],[0,3],[2,3],[3,3]]
期待値が3である4番目の店舗を選択し続けるのが最適解となります。

さっきのベルヌーイ分布の場合は事前分布がパラメータ２つのベータ分布となり更新がそれほど大変ではなかったのですが、平均・分散未知の正規分布の場合は事前分布がガウス・ガンマ分布となり、4つのパラメータを更新する必要が生じます。このあたりはベイズ推論による機会学習のp94~97に詳しく書いてあり、それを参考に実装しました。 (期待通りの結果がでたのでおそらく実装はあっているはず…)

from scipy.stats import t, norm, gamma

def thompson_gauss(count,m,beta,a,b,T,ps):
    reward=0
    cumulative_reward=[]
    
    for i in range(1,T):    
        thetas=[]
        for index in range(len(ps)):
            #事前分布からランダムサンプリング
            lambda_ = gamma.rvs(a[index], loc=0, scale=1/b[index])
            sigma_ = np.sqrt(np.reciprocal(lambda_*beta[index]))
            thetas.append(norm.rvs(loc=m[index], scale=sigma_,size=1)[0])
        
        #print(thetas,max(enumerate(thetas), key=lambda x: x[1])[0])
        
        #パラメータの更新
        index=max(enumerate(thetas), key=lambda x: x[1])[0]
        result = norm.rvs(loc=ps[index][0], scale=ps[index][1],size=1)[0]
        
        bf_m=m[index]
        bf_beta=beta[index]
        
        count[index]+=1
        beta[index]=beta[index]+1
        m[index]=(result+bf_beta*m[index])/beta[index]
        a[index]=0.5+a[index]
        b[index]=(result**2+bf_beta*bf_m**2-beta[index]*m[index]**2)/2+b[index]
        
        reward+=result
        cumulative_reward.append(reward)
    
    return pd.Series(cumulative_reward)/T

#試行回数
T=10000

#アームの数
armnum=4

#それぞれのアームの平均と分散
ps=[[0,0.3],[0,3],[2,3],[3,3]]

#パラメータ初期値
count=np.zeros(armnum)
m=np.zeros(armnum)
beta=np.ones(armnum)
a=np.ones(armnum)
b=np.ones(armnum)

thompson_gauss(count,m,beta,a,b,T,ps).plot()

事前分布からランダムサンプリングする部分はガンマ分布と正規分布を分けてサンプリングしていますが、 studentのt分布を用いても導出できるはずです。

f:id:rmizutaa:20190609213213p:plain

正規化した累積報酬は3に近くなり最適な選択が割とできているようです。

パラメータを確認します。

#パラメータの確認
params=pd.DataFrame()
params["count"]=count
params["m"]=m
params["beta"]=beta
params["a"]=a
params["b"]=b
params

f:id:rmizutaa:20190609213230p:plain

countがその店舗が選択された回数になります。期待値が最も大きい店舗3を選ぶことができていることが確認できます。

最後に事後分布を確認します。今度はstudentのt分布を使ってみます。

#予測分布
x = np.linspace(-1, 4, 1000)
plt.figure(figsize=(10,6))
for i in range(len(ps)):
    mu_=m[i]
    lambda_=beta[i]*a[i]/((1+beta[i])*b[i])
    neu_=2*a[i]   
    plt.plot(x,t.pdf(x, df=neu_, loc=mu_, scale=lambda_),label=i)
plt.legend()
plt.show()

f:id:rmizutaa:20190609213243p:plain

それぞれの期待値が比較的識別可能な形になっていることがわかります。試行回数が少ない1や2の店舗の期待値は少し本来のものとはずれることがあるようです。

メモ

事前分布の初期値は結果に影響が出そる可能性があるので、状況に応じて変化させたり最初に数回全ての選択肢を試した方がよい場合がありそう。
各分布のパラメータの意味をあまりわかっていなかったので教科書上のパラメータとpythonのstatsモジュールのパラメータの対応付けに苦労した。確率分布の勉強はもう一度やった方が良さそう。
人間には飽きがあるので、前回選択した店舗にはマイナス値の補正をかけるという方法をとるとより選択する店舗が分散するようになり実際のケースに近づけることができそうかと思った。

今回使用したコードは以下になります。
github.com

2019-05-21

ランチ最適化問題(秘書問題編)

python 数理最適化

はじめに

日々の生活を営む上で、ランチをどこで食べるかということは非常に重要な問題です。

ランチの選択肢としては、新しい店に入る（探索）と、今まで行ったことのある店で良かった店に入る（活用）のどちらかを行う必要があります。経験的に良かった店に入るのは比較的高い満足度を得ることができますが、未知でより良い店が近くにあるのを見逃している可能性があります。逆に新規の店に入る場合、その店が良い場合もありますが、あまり良くない店であることもあります。

より良いランチライフを送るためにはこの探索と活用をどう振り分けたらよいのでしょうか？

今回は、この問題を一般的に秘書問題や結婚問題とよばれる最適停止問題で考えてみたいと思います。

秘書問題について

wikiを読むとわかりやすいですが、秘書問題はn人の候補者から1人の最良の人物を採用したい場合、最初の37%の候補者は取らずにその中での最良の人物を覚えておき、それ以後にそれ以上の候補者が現れたらその人を採用することで37%の確率で最良の候補者を採用できるというものです。

この問題は現実問題として理解しやすいので数理モデルの入門書では頻出で37%という数字だけが強調されるのですが、この問題は下記のように比較的強い制約の元に成り立っています。

候補者全体の数が既知である
採用できるのは一人
最良の候補者しか考慮しない
候補者には順位がついており、単一指標で優劣を判定できる

現実問題に置き換える場合、これらの条件を少し変化させる場合があると思いますので、いろいろ条件を変えた時にこの37%という値はどう変化するのかを数値シミュレーションで確認していこうと思います。

実装

以下のサイトのコードを参考に数値シミュレーションを実装します。
https://imrankhan17.github.io/pages/Solving%20the%20secretary%20problem%20with%20Python.html

以下の4ケースの実験を行います。
1. 1位の店が選ばれる最適点(一般的な秘書問題)
2. n位以内の店が選ばれる最適点
3. 複数店舗選ぶ場合に最適な店が含まれる最適点
4. 複数店舗選ぶ場合の合計値の最適点

コードは上記サイトのものを少し変更しただけなのでここでは結果だけを載せていきます。

1位の店が選ばれる最適点(一般的な秘書問題)

f:id:rmizutaa:20190518203732p:plain

横軸が探索と活用の切り替え点、縦軸が1位の店が選ばれる確率になります。セオリー通り横軸も縦軸も約37%である点が最適となります。

n位以内の店が選ばれる最適点

１位に限定せずn位以内の店が選択できれば良いという場合です。 nが1,2,5,10の場合を示します。

f:id:rmizutaa:20190518203748p:plain

nが大きくなると探索を打ち切る点が左にずれ、またn位以内の店が選ばれる確率は上がります。もし10位以内でよければ15%くらいで打ち切るのが最も確率が良くなります。

複数店舗選ぶ場合に最良な店が含まれる最適点

１店ではなく複数店舗を選択することができ、その中で１位の店が選ばれる場合です。選択できる店舗数が1,2,5,10である場合の結果を示します。

f:id:rmizutaa:20190519194139p:plain

(私のコードが間違っていなければ)グラフは先ほどとかなり近しいものになりました。選べる店舗数が増えるにつれて最適点は左上にずれていきます。

5店舗選ぶ場合の合計値の最適点

最後に5店舗選択し、その合計値が少ない、つまり選んだ5店舗が全体的に最適となる点を探します。 5店舗の順位の合計値が20,30,40,50以下となる場合の確率を示します。

f:id:rmizutaa:20190518204441p:plain

順位の合計が20以下であって欲しい場合は15%前後、30-50の場合は10%前後で探索を打ち切るのが良さそうです。この条件で良い場合は早めに打ち切るのが良さそうです。例えば順位合計値30以下という条件で3ヶ月以内(90日)に５店を決定したいとなると、9日探索を行い、それ以後の81日の活用の際に探索時の最適店より良い店を採用していくのが最適解となります。それなりに良い店舗を5店選択することができれば快適な１週間のランチローテが組めそうですね。

メモ

心理学の実験では人はアルゴリズムの出す閾値よりも早く判断を下すという結果も出ているみたいだが、仮定の違いが原因で、実際は上位10%がとれればいいやくらいの感覚で人事採用をするので探索の打ち切り点が早めになってしまっているのではという可能性もあると思った。
途中で思ったが実際はランチ店探しは後戻り可能なので課題設定としてはあまり適しておらず、これを解きたいならバンディットアルゴリズムとかを使った方がいいんじゃないかと思った(次回)。

使用したコードは以下になります。 github.com

2019-05-09

CausalImpactの理解と実装

python 因果推論時系列解析

はじめに

今回はCausalImpactについて書いていきたいと思います。 CausalImpactはgoogle製の効果測定用パッケージで、主に広告やキャンペーンの効果を測定するのに用いられます。

なぜ広告やキャンペーンの効果を測定するのにこういうものが必要なのかというと、季節性や単なる流行の影響など測定したい項目以外にも様々な影響があるためにキャンペーン前と後を単純比較するだけではおかしな結果になることが少なからずあります。それを防ぐために因果推論を考える必要があり、CausalImpactはその因果推論の考えを使用したパッケージになります。

参考資料

論文:https://ai.google/research/pubs/pub41854
python実装:https://github.com/dafiti/causalimpact

causalimpactについて

論文を読んだ自分なりの理解をまとめます。
（解釈間違えてたらすみません）

従来のワークフロー（差分の差分法＋synthetic control method）

1つ以上の当てはまりが良さそうな対照群を選択する
synthetic control methodを用いて対照群を選択する(1が複数ある場合)
※synthetic control methodは複数の対照群の重みつけ和を処置群になるべく近づけることで、仮想の処置しなかった場合の処置群を作成する方法
差分の差分法を用いて処置群と2で作成した対照群を比較する

上記ワークフローの問題点

時系列データだとたいてい自己回帰成分が発生するが、差分の差分法では各時間の点が独立同分布であるという仮定を置いている
差分の差分法では２点間の違いしか見ることができないため、例えばキャンペーン期間が１週間あったとして、開始時や終了前の影響を個別に見ることができない。
synthetic control method→差分の差分法とおいう２段階の推計を行なっているので、どちらの段階の誤差の影響が大きいかがわかりづらい

CausalImpactの提案手法

状態空間モデルを用いて対照群から処置をしなかった場合の処置群を作成し予測値を算出。それを実際の処置群の値と比較することで因果効果を算出。

提案手法による改善点

状態空間モデルを使うことで自己回帰成分や季節性など時系列要因を考慮することができる
時系列の１点ごとの影響を確認することができる
synthetic control methodの部分と差分の差分法でやっていたことを１つの状態空間モデルでカバーしているためどの部分で誤差が発生しているかがわかりやすい。モデルの不確実性がわかる。

実装

causalimpactのオリジナルはRで書かれているのですが、それをpythonに移植したものがあったので今回はpython版を使用します。 python版のレポジトリは２つありますが、今回用いたのはdafitiさんの方です。

使用するデータは前回の差分の差分法をやったときと同じくRecruit Restaurant Visitor Forecastingのレストランの来店人数のデータを使い、ある店舗におけるお盆期間(8/11-20)の影響の効果を測定したいと思います。

2店舗のプロット図はこんな感じです。

f:id:rmizutaa:20190509080423p:plain

前処理をします。

df=pd.read_csv("air_visit_data.csv",parse_dates=["visit_date"])

#元のデータは欠損があるため日時のベースを作成
basedate=pd.DataFrame(list(pd.date_range('2016-05-01', '2016-08-20')))
basedate.columns=["visit_date"]

#店舗を指定、日時を限定
store1=df[df["air_store_id"]=="air_e55abd740f93ecc4"]
store1=store1[(store1["visit_date"]>="2016-05") & (store1["visit_date"]<="2016-08-20")]
store2=df[df["air_store_id"]=="air_1653a6c513865af3"]
store2=store2[(store2["visit_date"]>="2016-05") & (store2["visit_date"]<="2016-08-20")]

#データを結合
store1.rename(columns={"visitors":"visitors_store1"},inplace=True)
store2.rename(columns={"visitors":"visitors_store2"},inplace=True)
data=pd.merge(basedate,store1[["visit_date","visitors_store1"]],on="visit_date",how="left")
data=pd.merge(data,store2[["visit_date","visitors_store2"]],on="visit_date",how="left")
data=data.interpolate() #欠損値を線形補間
data=data.set_index("visit_date")

前処理後データはこんな感じです。

f:id:rmizutaa:20190509075343p:plain

CausalImpactに入れます。週の周期性があるためnseasonを7としています。

from causalimpact import CausalImpact
pre_period = ['2016-05-01', '2016-08-10']
post_period = ['2016-08-11', '2016-08-20']
ci = CausalImpact(data, pre_period, post_period,nseasons=[{'period': 7}],trend=True)
print(ci.summary())

f:id:rmizutaa:20190509075417p:plain

お盆の効果は平均すると13.7人、10日累積だと137人の効果があると出ました。差分の差分法でやったときは13.5人と出ていたので同じくらいの値が出ています。 95%信頼区間も算出されていて、累積で見ると48.0〜228.3と結構モデルが安定していないことがわかります。結果がどれだけぶれやすいかという不確実性が見れるのは良いですね。

グラフで見るとこのような形になります。

f:id:rmizutaa:20190509075444p:plain

１番目のグラフでyが処置群、Predictedが状態空間モデルによる予測値で、色がついている部分が予測値の信頼区間になります。２番目のグラフは1番目のグラフのy-Predictedを示しています。３番目のグラフは処置期間のy-Predictedの累積和を示します。

ちなみにCausalImpactはUnobservedComponentsを内包しており状態空間モデルそのものの結果を見ることもできます。

ci.trained_model.summary()

f:id:rmizutaa:20190509075601p:plain

作成した状態空間モデルの観測誤差が大きいために信頼区間が広めになっているようです。

CausalImpactは対照群を入力するのが通常ですが、対象群がない場合でも実行することができます。この場合状態空間モデルは処置群の処置前の系列から作成されます。

pre_period = ['2016-05-01', '2016-08-10']
post_period = ['2016-08-11', '2016-08-20']
ci = CausalImpact(data.iloc[:,0], pre_period, post_period,nseasons=[{'period': 7}])
ci.plot(figsize=(12, 6))

f:id:rmizutaa:20190509203704p:plain 今回の例だと対照群を入れた場合と結果はあまり変わらなかったりします。おそらく対照群が複数入力できる場合だと、そちらの方が結果が安定するんじゃないかと思います。

メモ

効果の信頼区間が出せるのはうれしい
１点ごとの推定ができるため処置区間内での変化も見ることができるのはよさそう
対象群が複数入力できない場合にはあまり効果を発揮できない可能性はあるかも
機会があれば使いたい

使用したコードは以下になります。

github.com

2019-05-01

差分の差分法(difference in difference)を試す

python 因果推論

はじめに

最初は最近話題(？)のCausalImpactについて書こうと思っていたのですが、その基礎となる差分の差分法（difference in difference）についての知識が不足していたため、この記事では差分の差分法について試したことを記述していきます。

差分の差分法とは

書いたことは下記資料の抜粋なので、より確実な情報が得たい方は下記の資料を参照してください。

参考資料：

以下の図を用いて説明します。

f:id:rmizutaa:20190501195352p:plain

出典：https://ja.wikipedia.org/wiki/%E5%B7%AE%E5%88%86%E3%81%AE%E5%B7%AE%E5%88%86%E6%B3%95

Pが処置群、Sが対照群で、それぞれの点は集団を示します。例えばTime1でP群のみに投薬を行い、Time2でその結果を検証するというケースがイメージしやすいかと思います。差分の差分法ではPとSが平行トレンドであることが条件となるため、Time2において仮にP1に処置が行われなかったとしたらその値はQになると想定されます。その仮定を用いることで、Time2におけるP2-Qを処置効果と捉えることができるようになります。

仕組みとしては結構簡単なのですが、差分の差分法を使う条件の処置群と対照群が平行トレンドであることが割とネックになります。この条件が結構厳しく、実験としてデザインされておらず気軽にデータを取り直せない環境下で処置群に対して平行トレンドをもつ対照群をどう選択するの？ということがこの手法を用いる上での課題になると思われます。(実施する可能性があるならデータ取得の部分にも関われということかもしれませんが)

計算するには下記の式で回帰分析を行えば良いみたいです。

$y= \beta _ {0}+ \beta _ {1} T+ \beta _ {2} S+\beta _ {3}(T \cdot S) + \beta _ {4} X +\varepsilon$

ここでTが処置群フラグ、Sが期間フラグ(図のTime1と2の違い)、T・Sは処置群*期間フラグで、この係数 $\beta _ {3}$ が求めたい処置効果になります。Xはその他の共変量で、ここを調整することで平行トレンド仮定を満たすような形に近づけることができるようです。

実験

kaggleのRecruit Restaurant Visitor Forecastingのレストランの来店人数のデータを使います。

ある店舗では立地的にお盆は来店人数が増えるという仮説があり、差分の差分法を用いてそうでない店舗と比較してどれくらいの来店人数の向上がみられるかを確認したいという課題を考えます。

とりあえずこの仮定に合いそうな2店舗を抽出します。期間はざっくり2016/5/1~8/20とします。抽出した2店舗の来客人数推移をプロットしたものを下記に示します。

f:id:rmizutaa:20190501195425p:plain

ここでstore1が処置群、store2が対照群で、store1ではお盆による集客効果があるように見えます。

データを回帰分析にかけられる形にするために前処理を行います。ここで、データに明らかな週の周期性があるためその情報も加えます。

#データ読み込み
df=pd.read_csv("air_visit_data.csv",parse_dates=["visit_date"])

#元のデータは欠損があるため日時のベースを作成
basedate=pd.DataFrame(list(pd.date_range('2016-05-01', '2016-08-20')))
basedate.columns=["visit_date"]

#店舗を指定、日時を限定
store1=df[df["air_store_id"]=="air_e55abd740f93ecc4"]
store1=store1[(store1["visit_date"]>="2016-05") & (store1["visit_date"]<="2016-08-20")]
store1["visitors"]=store1["visitors"].interpolate() #欠損を線形補間
store2=df[df["air_store_id"]=="air_1653a6c513865af3"]
store2=store2[(store2["visit_date"]>="2016-05") & (store2["visit_date"]<="2016-08-20")]
store2["visitors"]=store2["visitors"].interpolate() #欠損を線形補間

df=pd.concat([store1,store2])

#store1が処置群
store1["treatment"]=1
store2["treatment"]=0

#お盆(8/11-8/20)が処置期間
df["postperiod"]=(df["visit_date"]>="2016-08-11").astype(int)

#処置効果ダミー
df["treatmentXpostperiod"]=df["treatment"]*df["postperiod"]

#曜日ダミーの追加
weekdays=pd.get_dummies(df["visit_date"].dt.weekday).rename(columns=lambda x:f"weekday_{x}")
df=pd.concat([df,weekdays],axis=1)

この結果データはこのような形になります。

f:id:rmizutaa:20190501195445p:plain

線形回帰を行います。

import statsmodels.api as sm
X=df[['treatment', 'postperiod','treatmentXpostperiod','weekday_0', 'weekday_1', 'weekday_2',
       'weekday_3', 'weekday_4', 'weekday_5', 'weekday_6']]
X["coef"]=1 #切片
y=df["visitors"]
mod = sm.OLS(y,X)
res = mod.fit()
print(res.summary())

f:id:rmizutaa:20190501195534p:plain

処置効果であるtreatmentXpostperiodの係数は13.5245と比較的それっぽい値が出ました。立地的にこの店舗ではお盆の効果により14人ほど来店する人数が増えるようです。調整済み決定係数が0.355と当てはまりは悪いですが、係数のp値は0.05以下なのでそれなりの確からしさはあるかと思います。

平行トレンド仮定に基づくなら変数に使用した曜日と時間情報が同じであれば2店舗のトレンドは同様になるはずですが、平行になるのは数ではなく率ではないかという疑いもあり、そこの厳密性は少し欠けるかと思います。

また今回は時系列データを取り扱ったのですが、8/10以前と8/11以後という分け方しておらず、細かい前後関係を見られていないのは少し気になるところです。